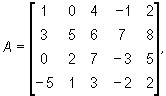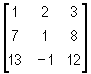Podstrona: Matematyka 2, ZiIP / Wizytówka pracownika PRz

Proszę rozwiązać zadania:

Ze strony http://prac.im.pwr.wroc.pl/~gewert/WYNIKI/lz-azga.pdf

zadania 7, 12 a i b, (w 12 stosując zwykłe wzory z deltą i zauważając, że np pierwiastek z -1 to  i, a więc pierwiastek z -4 to 2i   itd.  W zadaniu 7 przedstawić liczbę z jako x+iy i  pamiętać o tym, że liczby a+ib  oraz c+id  są równe tylko, gdy a=c  oraz b=d.

Dla poćwiczenia można rozwiązać zadania 13 i 14.

I. Ze strony http://prac.im.pwr.wroc.pl/~gewert/WYNIKI/lz-azga.pdf  proszę rozwiązać zadania:

9 (dla chętnych, wybrane przez siebie, na podstawie wykładu), 10 c,d,e na podst. wykładu i ćwiczeń, 11 a,b,c,d j.w,

II. Ze zbioru zadań Krysickiego i Włodarskiego "Analiza matematyczna w zadaniach I", zadania:

8.13, 8.14 (na podstawie wykładu i innych źródeł), 8.16, 8.17, 8.21*,  8.24-8.27.

Zadania w pliku pdf.

B=

Dla macierzy A i B proszę obliczyć  rząd.

Oprócz tego proszę rozwiązać zadania z Krysickiego: 9.23, 9.24, 9.93, 9.94* (proszę rozwiązać dla n=2,3, wymaga to wzoru na sinus i kosinus sumy kątów, który był na ostatnich ćwiczeniach), 9.101-9.103. Można też rozwiązać zadania, które pozostały z ostatnich ćwiczeń. 

Proszę rozwiązać zadania z Krysickiego:

9.97 i zauważyć, że to to samo, co zwykła macierz ale z katem (-a) zamiast a.)

9.99 (przynajmniej dla macierzy 3 x 3).

Jutro na wykładzie powinny być układy równań. Proszę spróbować rozwiązać układy spośród 9.57-9.66/. Pierwszy układ jest ukłdem Cramera. Pozostałe nie są, gdyż mają niekwadratowe macierze współczynników.

Ciekawą macierzą jest macierz Vandermonde'a. Jej wyznacznik jest nazywany wyznacznikiem Vandermonde'a. Dowody na jego wartość są np. w opracowaniu

https://www.mimuw.edu.pl/~torunczy/GAL/09-10/Sem1/IV-WYZN.pdf

Proszę przestudiować metodę eliminacji Gaussa na przykładach z załącznika i podobnie rozwiązać zadania z Krysickiego.  W drugim załączniku jest rozpatrywany układ sprzeczny, proszę również zapoznać się z takim zadaniem. Niektóe układy  ze zbioru są właśnie sprzeczne, można to sprzwdzić w odpowiedziach..

Proszę rozwiązać zadania ze strony http://prac.im.pwr.wroc.pl/~gewert/WYNIKI/lz-azga.pdf

51 - 57 oraz 58 a,b (c,d,e dla chętnych). Oprócz tego 59a. Dla chętnych proponuję zadanie 50 oraz zadania z układów równań z parametrem, czyli podpunkty a-e zadania 33.

Podaję kilka typowych zadań. Na kolokwium nie będzie ich aż tak dużo, prawdopodobnie 8 (3 z liczb zespolonych, 3 z algebry liniowej i 2 z gometrii).

Proszę przypomnieć obie pochodna. Zadania z rozwiązaniami są w rozdziale 6 Krysickiego i Włodarskiego. Dla chętnych zadania od 6.182, sa to funkcje szczególnego typu. Sposób obliczania tych pochodnych jest pokazany w przykładach 6.20 i 6.21.

Pochodne będziemy wykorzystywać do obliczania granic funkcji oraz przegiegu zmienności funkcji.

Poprawa będzie 15.01 w sali L-254 (budynek L-29) o godzinie 8:45.

Zadania z Krysickiegi i Włodarskiego:

A. Wyznaczyć przedziały monotoniczności i na tej podstawie także ekstrema funkcji z zadań:

10.58, 10.60, 10.63 - 10.69, 13.12, 13.15, 13.31, 13.33.  Uwaga: treści zadań w zbiorze sa szersze.

B. Zadania tzw. optymalizacyjne: 10.143 - 10.145

   Podaję  kilka typów zadań. Najlepiej, gdyby Państwo rozwiązali wszystkie. Możemy niektóre rozwiązać na kolejnych zajęciach, np. te, które  nie będą chciały wyjść. Wykresy funkcji, a nawet asymptoty można obejrzeć w programie (bezpłatnym) na stronie wolframalpha.com.

Wysyłam przykłady, są to dwa zadania, w których są najczęstsze błędy. Zadanie drugie jest trochę inne niż na kolokwium, ale  może pokazać, że sposób rozumowani jest ważny.

Można rozwiązywać zadania ze zbioru zadań Krysickiego i Włodarskiego, 15.23 - 15.82 (niektóre rozwiązaliśmy na zajęciach). 

W pierwszej kolejności proszę rozwiązać zadania z tego rozdziału 15 o numerach:

27, 28, 31, 34, 38 - 48, 53, 56, 59, 61 - 63, 65, 74, 76, 79.  Tylko w zaaniach 61, 74, 76 i 79 z tej postatniej grupy stosujemy metodę przez części (61 - najpierw podstawienie), w pozostałych podstawienie lub Lemat z ćwiczeń (ten Lemat również w zadaniu 74).

Zadania są z rozdziału 16 Krysickiego & Włodarskiego:

28, 29, 36 i 41 (postać kanoniczna i wzór z logarytmem z ćwiczeń lub wykładu - chodzi o sytuację niewygodnej delty),

45, 47, 57, 61, 67, 68 (rozkład minownika na czynniki np. metodą grupowania wyrazów lub z tw. Bezout), 69 (wzór rekurencyjny z wykładu w semestrze I), 70 i 73 (najpierw trzeba wykonać dzielenie wielomianów), 77, 84* (trzeba rozłożyć mianownik na iloczyn dwóch trójminów kwadratowych). Zadania 89 i 91 zrobimy na ćwiczeniach, ale jak ktoś chce, to można zobaczyć, jak takie zadania sa rozwiązywane w zbiorze zadań - np.  zadanie 16.23, rozwiązane szczegółowo w zbiorze.

     Zadania są w załączniku - konkretne całki i numery zadań ze zbioru.

Zostało kilka zadań z całek z pierwiastkami i te zadania rozwiążemy na początku. Metody były dokładnie pokazane na wykładzie.

Dla chętnych wysyłam link do całek z różniczek dwumiennych - do poćwiczenia (są to zadania wg autorów strony średnio trudne i trudne, te ostatnie to ostatni rozpatrywany na wykładzie typ):

https://www.zadania.info/d1049/1/5_1

O ile zdążymy, to w dalszej kolejności będą całki trygonometryczne - rozdział 18, zadania:

41, 49, 50, 59 (trzeba zgadnąć podstawienie), 77 (UPT 1), 78 (UPT 1), 81 (UPT 1), 83 (UPT 2), 87 (UPT 2).

Pozostałe typy całek trygonometrycznych będą jeszcze na wykładzie.

1.  Zostały jeszcze zadania z ostatnich ćwiczeń.

2.  Proszę znaleźć w zbiorze zadań przykłady, jak rozwiązać zadania kolejnych typów. Są to przykłady 18.10, 12 i 17.  Zadania z nimi związane to zadania 62 - 70. Można wybrać sobie kilka z nich.

3. Zadania 18.30 - 38 można rozwiązać, całkując 2 razy przez części, albo tak, jak w przykładzie 18.2.

4 . Wstępnie zarezerwowałem salę L-341 na środę,  na godzinę 12:15.  Nie jest ona zatwierdzona, ale w planie ją widać, więc nikt nie powinien tej sali zająć.Można więc przyjść włąśnie o tej godzinie.

Tym razem zadania są ze strony http://prac.im.pwr.wroc.pl/~gewert/WYNIKI/lz-am1.pdf

1. Zad. 60 - dla chętnych. Tu podział przedziału jest na odcinki tej samej długości.

2. Zad. 62, wybrany podpunkt. Zadanie polega na zauważeniu, że ciąg z lewej strony to suma całkowa pewnej funkcji, a następnie wykorzystaniu wzoru Newtona-Leibniza. Np. w zadaniu a) jest funkcja f(x)= x^3 na przedziale [0,1].

3. Zad. 75. Należy znaleźć granice całkowania i całkować funkcje albo ich różnice, jak na ćwiczeniach. 

Np. w a) wychodzi przedział  całkowania [0,1], w b) [-2,2], w c) [1/e,e]. Proszę dojść do tego samodzielnie. W zad. e) lepiej całkować po dy, albo odbić obszar względem prostej y=x i wtedy całkować normalnie.

4. Zad. 76. Proszę znaleźć wzór na długość krzywej w zbiorze zadań na przykład i rozwiązać zadania a) i e).

5.. Krysicki, Włodarski, zad. 19.37 - 19.53. Można wybrać kilka i rozwiązać, by nabrać wprawy. 

Oprócz zadań, które zostały z poprzednich  2 zajęć, są nowe zadania:

ze strony http://prac.im.pwr.wroc.pl/~gewert/WYNIKI/lz-am1.pdf,

zad. 76 b, c

zad 77 a, e, f.

Podaję typowe zadania na kolokwium. Będą 3 całki łatwe, 3 trudniejsze oraz 2 zadania z zastosowań geometrycznych.

Termin 8.05. Zajęcia sprzed Świąt zostały przełożone na 15  maja i będą wtedy 4 godziny ćwiczeń - przerobimy funkcje wielu zmiennych.

Zadania są takie, jak były na ćwiczeniach. Krysicki, Włodarski, tom 2. 

Zadania 1.113, 1.118, 1.120, 1.125, 1.131, 1.138 (uwaga tam jest błąd w treści i ma być na końcu y^2 a nie y). W tym ostatnim zadaniu, w punkcie (0,0) hessian zeruje się i wtedy trzeba wziąć pod uwagę oś oy i potem prostą y=x w dziedzinie funkcji. Wtedy łatwo yciągnąć wniosek, czy jest tam ekstremum czy nie.

Kolejne zadania to wartość maksymalna lub minimalna funkcji.

1.140 (wzór na pole trójkąta P=2R^2sin a sin b sin(pi-a-b))

1.142. Wskazówka: pole ma wartość największą, gdy kwadrat pola ma wartość największą. Wtedy łatwo wychodzi odpoiedź po zastosowaniu wzoru Herona. 

Dla chętnych - można zgłosić się z tymi zadaniami - przykłady rozwiązane w zbiorze: 1.152, 1.153.

Dodatkowo zamieszczam dość szczegółowe rozwiązanie zadania z ćwiczeń. Niektóre obliczenia pominąłem.

Proszę rozwiązać zadania ze zbioru Krysickiego i Włodarskiego, tom 2:

-  z rozdziału 7, zadania 19, 24, 29, 34, 39, 40, 66 i 67 (ostatnie 2 to równania z warunkiem początkowym);

-  z rozdziału 8 proszę przeczytać początek paragrafu 8.1, aż do Przykładu 8.1 włącznie, jest to typ, którego jeszcze nie omawialiśmy, do tego jeszcze zadania 8.3 i 8.14.;

-  z tego samego rozdziału zadania z równań jednorodnych względem x i y, a więc zadanie 22 (obie strony najpierw trzeb podzielić przez x) oraz 40 (obie strony dzielimy przez x^2); po tym podzieleniu zobaczymy zależność tylko od y/x. 

Zadania z równań różniczkowych są w pliku.

Prosze rozwiązać zadania  nierozwiazane z ostatniej listy oraz równania liniowe rzędu 1:

9.22, 9.24, 9.31, 9.42.

oraz równania liniowe jednorodne rzędu 2: 

13.8, 13.20 i 13.23 (każde innego typu).

Ponadto prosze zapoznać się z rozdziałem 9.4 ze zbioru Krysicki, Włodarski, tom II. Chodzi o metodę przewidywania. Można przeczytać pierwszy przypadek z funkcją wykładniczą po prawej stronie lub więcej, w miarę możliwości. Wszystkie przypadki będziemy rozpatrywać w odniesieniu do równań rzędu 2.

Zagadnienia są w załączniku.

Zagadnienia są podane w pliku. Na egzaminie będzie mozliwość zanotowania wypowiedzi. Proponuję termin 26.06 - w środę, początek: godzina 9, sala 317.

Zaliczenie dla grupy C1 - 25.06, godz. 15, sala L 219. 

Egzamin na wyższą ocenę - 26.06, godz 10, sala L-317

Egzamin dla osób z nieobecnościami na wykładzie - 26.06, godz.9, sala L-317 (mozliwa godzina późniejsza, np. 12)

W drugim tygodniu sesji również będą możliwe powyższe zaliczenia i egzaminy

Dowolnie wybrane zadania, głównie z równań różniczkowych rzędu 2, ale tez z innych równań różniczkowych.

Przesyłam zestaw zadań z rozwiązaniami. Uwaga do zadania 3a. Rozwiazaniem jest jeszcze funkcja y=0 (po drodze było dzielenie przez y).

Wyniki podałem w materiałach dla zalogowanych. Większość osób zaliczyła.

Zaliczenie: wtorek o 14:30, sala L 317. Mozna zaliczać wszystkie działy.

Egzaminy ustne w środę rano (od 9) lub we wtorek na konsultacjach ()13:30 - 14:30) lub  po zaliczeniu, czyli około godziny 16.

W tym tygodniu jestem w poniedziałek i wtorek. W poniedziałek 14-15:30, a e wtorek 8:30-10   mam konsultacje, można wtedy przyjść na egzaminy ustne. Zaliczenie pisemne najlepiej po konsultacjach. Można przyjść pod pokój 108e, salę znajdziemy.  Jeżeli ktoś ma więcej działów do zaliczenia, można to zrobić na raty.

Zachęcam do egzaminu na wyższą ocenę. Oceny wpisane w  USOS-ie można jeszcze poprawić.